Aptitude Questions – Data Interpretation Set 87

Hello Aspirants.

Welcome to Online Quantitative Aptitude section in AffairsCloud.com. Here we are creating question sample From Data Interpretation based on latest pattern that is important for SBI, IBPS, RBI, SSC , NICL, LIC and other exams. We have included Some questions that are repeatedly asked in exams.

I. Study the following graph carefully to answer the given questions

Time taken by the pipes to fill a tank/cistern (hours/minutes)

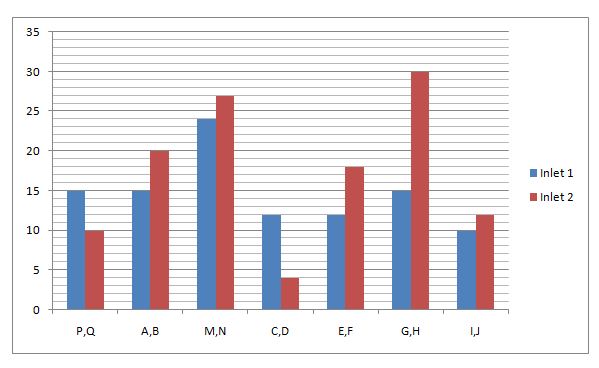
1. A large cistern can be filled by two pipes P and Q. How many minutes will it take to fill the Cistern from an empty state if Q is used for half the time and P and Q fill it together for the other half?
   A. 6.5 minutes
   B. 7.5 minutes
   C. 8.5 minutes
   D. 9.5 minutes
   E. None of the Above
   
   Answer & Explanation

   Answer – B. 7.5 minutes
   Explanation :
   Part filled by P and Q = 1/15 + 1/10 = 1/6
   Part filled by Q = 1/10
   x/2(1/6 + 1/10) = 2/15 = 15/2 = 7.5 minutes
   
   
2. Two pipes M and N can fill a tank. If both the pipes are opened simultaneously, after how much time should N be closed so that the tank is full in 8 minutes?
   A. 14 minutes
   B. 12 minutes
   C. 15 minutes
   D. 18 minutes
   E. None of the Above
   
   Answer & Explanation

   Answer – D. 18 minutes
   Explanation :
   Required time = y(1-(t/x)) = 27(1-(8/24))= 18 minutes
   
   
3. Three pipe E, F, and R can fill a tank. If Pipe R alone can fill a tank in 24 minutes then the pipe R is closed 12 minutes before the tank is filled. In what time the tank is full?
   A. 8.(5/13)
   B. 8.(4/13)
   C. 7.(4/13)
   D. 8.(6/13)
   E. None of these
   
   Answer & Explanation

   Answer – B. 8.(4/13) 
   Explanation :
   Let T is the time taken by the pipes to fill the tank
   (1/12 + 1/18 + 1/24)*(T – 12) + (1/12 + 1/18)*12 = 1
   We will get T = 108/13 = 8.(4/13)
   
   
4. Two pipes C and D can fill a cistern. If they are opened on alternate minutes and if pipe C is opened first, in how many minutes will the tank be full?
   A. 4 minutes
   B. 5 minutes
   C. 2 minutes
   D. 6 minutes
   E. None of the Above
   
   Answer & Explanation

   Answer – D. 6 minutes
   Explanation :
   Pipe P can fill = 1/12
   Pipe Q can fill = 1/4
   For every two minutes, 1/12 + 1/4 = 1/3 Part filled
   Total = 6 minutes
   
   
5. Two pipes, A and B are opened simultaneously and it is found that due to the leakage in the bottom, 17/7 minutes are taken extra to fill the tank. If the tank is full, in what approximate time would the leak empty it?
   A. 27 minutes
   B. 32 minutes
   C. 36 minutes
   D. 39 minutes
   E. None of these
   
   Answer & Explanation

   Answer – D. 39 minutes
   Explanation :
   Total time taken by both pipes before the leak was developed = 60/7 minutes
   now, leaks is developed which will take T time to empty the tank so, (1/15 +1/20 – 1/T) = 1/11
   solve for T, we will get 660/17 minutes = 39 minutes (approx.)
   
   
6. A waste pipe, W can carry off 12 litre of water per minute. If all the pipes I, J and W are opened when the tank is full and it takes one hour to empty the tank. Find the capacity of the tank.
   A. 30
   B. 45
   C. 60
   D. 75
   E. None of these
   
   Answer & Explanation

   Answer – C. 60
   Explanation :
   Let the waste pipe take ‘T’ time to empty the tank.
   (1/10 + 1/12 – 1/T)*60 = -1
   We will get T = 5 min
   So capacity = 5*12 = 60ltr
   
   
7. Two pipes G, and H are opened and when the tank is 1/3 full a leak is developed due to which 1/3 water supplied by the pipe leaks out. What is the total time to fill the tank?
   A. 20/3 minutes
   B. 35/3 minutes
   C. 40/3 minutes
   D. 50/3 minutes
   E. None of these
   
   Answer & Explanation

   Answer – C. 40/3 minutes
   Explanation :
   (1/15 + 1/30)*T1 = 1/3, T1 = 10/3 minutes
   Now after leak is developed, [(1/15 + 1/30) – (1/3)*(1/15 + 1/30)]*T2 = 2/3
   T2 = 10 minutes. So total time = 10 + 10/3 = 40/3 minutes
   
   
8. Two pipes E and F are opened simultaneously and it is found that due to leakage in the bottom of the tank it took 48 minutes excess time to fill the cistern. When is the cistern full, in what time will the leak empty it?
   A. 72 hours
   B. 62 hours
   C. 64 hours
   D. 84 hours
   E. None of the Above
   
   Answer & Explanation

   Answer – A. 72 hours
   Explanation :
   Work done by the two pipes in 1 hour = (1/12)+(1/18) = (15/108).
   Time taken by these pipes to fill the tank = (108/15)hrs = 7 hours 12 min.
   Due to leakage, time taken = 7 hours 12 min + 48 min = 8 hours
   Work done by two pipes and leak in 1 hour = 1/8.
   Work done by the leak in 1 hour =(15/108)-(1/8)=(1/72).
   Leak will empty the full cistern in 72 hours.
   
   
9. Three pipes C, A and B can fill a tank. If pipe C is opened all the time and pipe A and B are opened for one hour alternatively. The tank will be full in
   A. 5hr
   B. 6hr
   C. 7hr
   D. 8hr
   E. None of these
   
   Answer & Explanation

   Answer – C. 7hr
   Explanation :
   (1/12 + 1/15) + (1/12 + 1/20) = 17/60 (in 2 hrs this much tank is filled)
   so in 6 hrs 51/60 is filled. Remaining, 9/60 = (1/12 + 1/15)*t, so T = 1hr
   so total = 6 + 1 = 7 hr
   
   
10. Three pipes R, P and Q can fill the tank. R can fill the tank 5 minutes less than that of Q. If all the pipes are opened together and pipe P is turned off 5 minutes before the tank is filled. Then find the time in which the tank will full.
    A. 45/11hrs
    B. 53/11hrs
    C. 51/13hrs
    D. 47/11hrs
    E. None of these
    
    Answer & Explanation

    Answer – A. 45/11hrs
    Explanation :
    Let total time taken by the pipes is T hrs, then
    (1/5 + 1/10 + 1/15)*(T – 5) + (1/5 + 1/15)*5 = 1