Quadratic Equation

aX²+bX +c =0

a = coefficient of X²

b = coefficient of X

c = constant term

There will be five problems from this topic. It is the easiest one, so you can solve all problems within 5 to 7 minutes.

In this kind of problems two equations will be given as question, you have to solve the equation and find the relation between them

1.P > Q

2.P < Q

3.P ≥ Q

4.p ≤ Q

5.P = Q or relationship cannot be established

Example 1:P²+13P+40=0

                  Q²+7Q+12=0

Step1: let us take equ 1. P²+13P+40=0 in this equation coefficient of p, 13 should be split into two numbers in such a way that multiplication of both numbers should be equal to constant term 40 and addition of numbers should be equal to 13

13 can be split into (1,12) (2,11) (3,10) (4,9) (5,8) (6,7)

In these combination 5 and 8 only can give 40 while multiplying, so this is the number we are searching for,and since the coefficient of P² is 1 and there is no negative sign in the equation, we can directly write value of P by simply changing the sign

 P= -5,-8

( just for reference Actual procedure is  P²+5P+8P+40=0

P(P+5)+8(P+5)=0

(P+5)(P+8)=0

P=-5,-8 )

Step 2: Now equ2. Q²+7Q+12=0 similar process applicable for this equation to find Q, here coefficient of Q should be split into two numbers and multiplication of the numbers should give 12

7 can be split up into (1,6) (2,5) (3,4)

Combination of 3 and 4 alone satisfy our need i.e. giving 7 and 12 while adding and multiplying the numbers respectively, since there is no negative sign in the equation,we can directly write value of Q by changing sign .

Q=-3, -4

P= -5,-8

Obviously P < Q

Example 2: 2p²+12p+16=0

                   2q²+14q+24=0

Step 1: let us take equ1 since coefficient of p² is 2,we have to multiply 2 with constant number 16 , now as usual 12 should be split up into two numbers and multiplication of the numbers should give ( 2*16=) 32 .

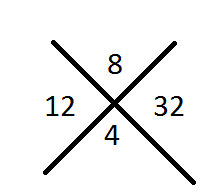
4+8 =12

4*8=32

 12 can be split up into 4 and 8,

 now change the sign of numbers and divide it by 2 since the coefficient of p² is 2 ,

Thus the value of  p = -2,-4

Step 2: now take equ2. And follow the same procedure multiply 2 with constant number 24 . So addition of two numbers should be 14 and multiplication of numbers should be 48 (24*2)

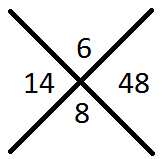
6+8 =14  ;  6*8=48

Numbers are 6 and 8, now divide by 2, since the coefficient of q² is 2 so the value of q is -3,-4

here, one of the numbers of p and q are same but other number of p is greater than other number of q 

so ans is p ≥ q

If you have doubt in finding which one is greater, use this technique.

Number which is 1^st from right hand side is greater one.

Example 3:  x²-x-6=0

                    2y²+13y+21

Step1: Here constant number and coefficient of x are negative so the combination of numbers will be positive and negative.

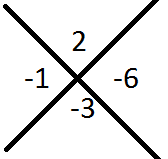
Combination is 2,-3

Value of x=-2 , 3

Step2: proceed with equation 2

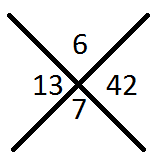
Combination is (6,7) ,

since the coefficient of y² is 2 divide the value of y by 2  

Y=  -(6/2) , -(7/2)

Y= -3 , -3.5

Relation is X > Y

Example 4: 12x²+11x+12=10x²+22x

                  13y²-18y+3=9y²-10y

Step1: convert this into normal quadratic equation form

2x²-11x+12=0

4y²-8y+3=0

Step2: now as usual normal procedure , here coefficient of x is negative and constant term is positive so both numbers will be negative

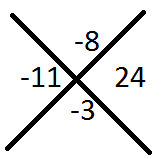
 Combination is -8,-3

And value of x= 4, 3/2

 Step3: proceed with equ 2

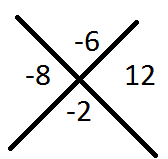
Combination is (-2,-6)

since coefficient of y² is 4 divide the value of y by 4 ,

And value of y = ½ , 3/2

 Relation is x ≥ y

 Example 5: 18/x² + 6/x -12/x² = 8/x²

                    Y³+9.68+5.64 =16.95

Multiply x² in equ1 it becomes 18+6X -12 =8

Solving this equations we get x = 1/3 = 0.33

Solving equ2 we get y³ = 1.63

          Y = 1.17

Relation is x < y

Example 6: (x+18)^1/2 = (144)^1/2 – (49)^1/2

                   Y² +409 = 473

By solving equ1, we get x = 7

Solving equ2 we get y = ± 8

Relation cannot be formed between x and y since x is both highest and lowest one.

TIPS to find combination:

1. If the coefficient of x or y and constant term is negative, then one number will be positive and other will be negative.
2. If the coefficient of x or y and constant term is positive, combination will be positive.

3. If the coefficient of x or y and constant term are positive and negative then the combination of numbers will be both positive and negative.