IBPS Clerk Prelims: Quants Day 3

Hello Aspirants. Welcome to Online Quant Section in AffairsCloud.com. We are starting IBPS Clerk course 2015 and we are creating sample questions in Quantitative Aptitude section, type of which will be asked in IBPS Clerk Prelims Exam.

Stratus – IBPS Clerk Course 2015 

• IBPS Clerk Daily Test Questions
• IBPS Clerk Practice Test Questions

[flipclock]

Directions (1-5): Study the following pie-charts and answer the questions that follow: There are 5 sections in a class with given information in the pie-char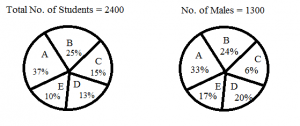

1. Find the ratio of the total number of students in sections C and D to number of males in the same sections. A) 336 : 169 B) 313 : 169 C) 360 : 147 D) 336 : 149 E) None of these
   Answer

   A) 336 : 169 Explanation: Students in C and D = (15+13)/100 * 2400 = 672 No of males in C and D = (6+20)/100 * 1300 = 338 So ratio = 672 : 338 = 336 : 169
   
   
2. What is the average number of females in sections A and C? A) 370.5 B) 334 C) 384.5 D) 390.5 E) 357
   Answer & Solution

   B) 370.5 Explanation: Students in A and C = (37+15)/100 * 2400 = 1248 No of males in A and C = (33+6)/100 * 1300 = 507 So females in A and C = 1248 – 507 = 741, so average = 741/2 = 370.5
   
   
3. Find the angle subtended by C section in the total number of students diagram. A) 72^o B) 55^o C) 60^o D) 54^o E) 57^o
   Answer & Solution

   D) 54^o Explanation: 15/100 * 360 = 54^o
   
   
4. Find the ratio of the number of males in D section to the females in section E. A) 260 : 191 B) 260 : 137 C) 460 : 19 D) 260 : 21 E) 260 : 19
   Answer & Solution

   E) 260 : 19 Explanation: Males in D = 20/100 * 1300 = 260 Students in E = 10/100 * 2400 = 240, males in E = 17/100 * 1300 = 221, so females in E = 240 – 221 = 19 Ratio = 260 : 19
   
   
5. What is the number of females in sections A and B? A) 740 B) 747 C) 737 D) 741 E) 742
   Answer & Solution

   B) 747 Explanation: Students in A and B = (37+25)/100 * 2400 = 1488 Males in A and B = (33+24)/100 * 1300 = 741 So females = 1488 – 741 = 747
   
   
6. A mixture contains A and B in the ratio of 5 : 3. 16 litres of this mixture is taken out and 5 litres of A is poured in. the new mixture has ratio of A to b as 11 : 6. Find the total original quantity of mixture. A) 80 litres B) 96 litres C) 98 litres D) 84 litres E) 92 litres
   Answer & Solution

   B) 96 litres Explanation: A = 5x, B = 3x After taking out 16 l of mixture, A = 5x – 5(5+3) * 16 = 5x – 10 B = 3x – 3(5+3) * 16 = 3x – 6 After pouring 5 l of A, A = 5x – 10 + 5 = 5x – 5 So now, 5x-5/3x-6 = 11/6 Solve, x = 12 Total original quantity = 5x+3x = 8x = 8*12 = 96 litres
   
   
7. A bag contains 3 white balls, 5 black balls and 4 yellow balls. 3 balls are drawn at random. What is the probability that atmost 1 ball is black in color? A. 5/22 B. 2/9 C. 8/11 D. 7/11 E) None of these
   Answer & Solution

   D. 7/11 Explanation: Atmost 1 black means 0 black or 1 black Case 1 : none is black None is black means 3 balls from 7 balls (3 w + 4 y), ways are ⁷C₃ = 7*6*5/3*2*1 = 35 Case 2: 1 ball black and other 2 white or yellow Ways are ⁵C₁ × ⁷C₂ = 5 * 7*6/2*1 = 105 There are a total of 12 balls. Ways for drawing 3 balls is ¹²C₃ = 12*11*10/3*2*1 = 220 So required prob. = 35+105/220 = 140/220 = 7/11
   
   
8. A man reaches at 10 AM from P to Q when his average speed is 15 km/hr and reaches at 12 noon when the average speed is 10 km/hr. What should be the average speed to reach at 9 AM? A. 18 km/hr B. 20 km/hr C. 22 km/hr D. 25 km/hr
   Answer

   B. 20 km/hr Explanation: Let distance from P to Q is ‘d’ and time taken to reach at 9 AM is ‘t’ Then with 10 AM, time becomes ‘t+1’, so d/(t+1) = 15 With 12 noon, time becomes ‘t+3’, so d/(t+3) = 10 Solve the equations, t = 3 hrs, d = 60 km So speed to reach at 9 AM = 60/3 = 20 km/hr
   
   
9. A and B started a business by investing Rs 6400 and Rs 4600 respectively. After 4 months both withdraw Rs 400 and C joined them with Rs 8000. At the end of year, what will be the ratio of their profits? A) 92 : 55 : 80 B) 92 : 65 : 80 C) 72 : 25 : 56 D) 80 : 57 : 44 E) None of these
   Answer & Solution

   B) 92 : 65 : 80 Explanation: A’s share : B’s share : C’s share 6400*4 + 6000*8 : 4600*4 + 4200*8 : 8000*8 Two 0’s get cancelled, we are left with 64*4 + 60*8 : 46*4 + 42*8 : 80*8 We can see that 8 gets cancelled from each term, now left with 32 + 60 : 23 + 42 : 80 92 : 65 : 80
   
   
10. A’s age 8 years ago was four less than B’s age that time. Ratio of A’s age 8 years after and B’s age that time will be 6 : 7. Find the ratio of A’s age after 4 years to that of B’s age at that time. A) 2 : 5 B) 3 : 4 C) 5 : 7 D) 6 : 5 E) 5 : 6
    Answer

    E) 5 : 6 Explanation: Let the present ages of A and B are x and y respectively. 8 years ago, x-8 = (y-8) – 4. This gives x – y = -4 After 8 years, x+8/ y+8 = 6/7. This gives 7x – 6y = -8 Solve both equations, x = 16, y = 20 So required ratio = (16+4) : (20+4) = 20 : 24 = 5 : 6