Let’s solve some Coded Inequality Problems
Directions
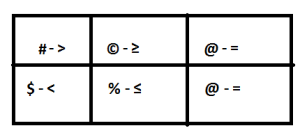
P © Q means P is not smaller than Q
P % Q means P is not greater than Q
P # Q means P is neither smaller than nor equal to Q
P @ Q means P is neither greater than nor smaller than Q
P $ Q means P is neither greater than nor equal to Q
Let’s form a table first.
Problem 1
Statements F % T, T @ J, J # W.
Conclusions 1) J @ F. 2) J # F. 3) W $ T.
Modified Statement: F % T @ J # W
Conclusions
1. J @ F – Reverse Line. Symbols are @ and %. Higher priority is %. Since it is Reverse line we should look the symbol opposite to %. i.e. ©. Conclusion 1 is False.
2. J # F – Reverse Line. Symbols are @ and %. Higher priority is %. Since it is Reverse line we should look the symbol opposite to %. i.e. ©. Conclusion 2 is False.
3. W $ T – Reverse Line. Symbols are # and @. Both symbols are in Row 1. High priority goes to #. Since it is a reverse line, we should note the symbol opposite to #. i.e. $. Conclusion 3 is True.
NOTE
If we look above, both conclusions 1 and 2 are false. Now check for Merging concept. They have similar characters. Both are false. Now try to combine or merge the symbols of the conclusions. If we merge @ and #, we will get ≥. So it forms a meaningful conclusion.
So, Only either 1 or 2 and 3 are true.
Problem 2
Statements – R # D, D © K, K $ M.
Conclusions – 1. M # R. 2. K $ R. 3. D # M
Modified Statement – R # D © K $ M

Conclusions
1. M # R – Reverse Line. Symbols – $, ©, and #. They are in different rows. FALSE
2. K $ R – Reverse Line. Symbols – © and #. Both are in Row 1. # is higher priority. Symbol opposite to # is $. So TRUE.
3. D # M – Forward line. Symbols – © and $. Different Rows. So False.
We cannot apply merging concept here, as the characters are different.
Only Conclusion 2 is True
Problem 3
Statements – Z © F, F $ M, M % K
Conclusions – 1) K # F. 2) Z # M. 3) K # Z.
Modified Statement: Z © F $ M % K

Conclusions
1) K # F – Reverse Line. Symbols are % and $. High Priority – $. Symbol opposite to $ is #. TRUE.
2) Z # M – Forward Line. Symbols are © and $. Different Rows. FALSE
3) K # Z – Reverse Line. Symbols are %, $, and ©. Different Rows. False.
Only Conclusion 1 is True.
Problem 4
Statement – H @ B, B © R, A $ R
Conclusion – 1. B © A 2. R % H. 3. A $ H
Modified Statement H @ B © R # A.
(In previous problems it was in a sequence and we easily combined the statements. When there is change in sequence, we should change the symbol and write it in a sequence.)
Here, Second statement is B © R and third Statement is A $ R. To combine these two, we should change the third statement as R # A. (# is opposite to $). Now we can combine them as B © R # A.
Modified Statement H @ B © R # A

Conclusions
1. B © A – Forward Line. Symbols between B and A are © and #. High Priority is #. FALSE
2. R % H – Reverse Line. Symbols – © and @. High Priority for ©. Opposite to © is %. TRUE
3. A $ H – Reverse Line. Symbols – #, ©, and @. High Priority for #. Symbol opposite to # is $. So True.
Conclusions 2 and 3 are True.
NOTE: When a conclusion forms Forward line, just look for the highest priority symbol. When a conclusion forms Reverse Line, look for the symbol which is opposite to the highest priority symbol.