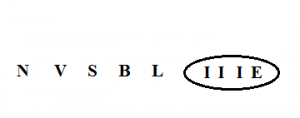Hello Aspirants. Welcome to Online Reasoning Section in AffairsCloud.com. Here we are creating question sample in coded Permutations & Combinations, which is common for all the competitive exams. We have included Some questions that are repeatedly asked in bank exams !!
- In how many ways 5 rings can be worn on 3 fingers?
A) 15
B) 120
C) 60
D) 70
E) 243C) 60
Explanation:
0 0 0
Let these 3 circles are 3 fingers
For 1st finger we have 5 choices, for second finger we have 4 choices left of rings, for third finger we have 3 choices left.
So total 5*4*3 = 60 ways - In how many ways the letters of the word ‘AUTHOR’ be arranged taking all the letters?
A) 120
B) 720
C) 360
D) 60
E) None of theseB) 720
Explanation:
AUTHOR contains 6 letters, so total 6! ways. - In how many ways the letters of the word ‘MINIMUM’ be arranged taking all the letters?
A) 420
B) 840
C) 5040
D) 720
E) 360A) 420
Explanation:
MINIMUM contains 7 letters, so total 7! ways. But it contains 2 I’s and 3 M’s so divide by 2! And 3!
So ways 7!/(2! * 3!) = 7*6*5*4*3*2*1 / 2*1*3*2*1 = 420 - How many words of 4 letters with or without meaning be made from the letters of the word ‘LEADING’, when repetition of letters is allowed?
A) 4808
B) 57600
C) 2401
D) 57624
E) None of theseD) 57624
Explanation:
LEADING is 7 letters.
We have 4 places where letters are to be placed.
For first letter there are 7 choices, since repetition is allowed, for second, third and fourth letter also we have 7 choices each, so total of 7*7*7*7 ways = 2401 ways.
Now for arrangement of these 4 words, we have 4! Ways.
So total of 2401 * 4! Ways. - In how many ways letters of word ‘INVISIBLE’ be arranged such that all vowels are together?
A) 2560
B) 2880
C) 5040
D) 2520
E) 720B) 2880
Explanation:
First make IIIE in a circle. So we have
Now we have N, V, S, B, L and box, their arrangements can be done in 6!
Letters inside circle are also to be arranged, we have I, I, I, E so ways are 4!/3!
Total ways 6! * 4!/3! - How many words can be made out of the letters of word ‘POUNDING’ such that all vowels occupy odd places?
A) 1440
B) 1400
C) 7200
D) 5600
E) 40320A) 1440
Explanation:
In POUNDING, there are 8 places
1 2 3 4 5 6 7 8
So for 3 places selection of vowels, we have 1, 3, 5, 7 number places 4C3 ways
Now for arranging these 3 vowels, ways are 3!
Remaining 5 are consonants (in which there are 2 N’s) for which 5!/2!
so total ways = 4C3*3!*(5!/2!) - In how many ways a group of 2 men and 4 women be made out of a total of 4 men and 7 women?
A) 720
B) 210
C) 420
D) 360
E) 120B) 210
Explanation:
We have to select 2 men from 4 men, and 4 women from 7 women
So total ways = 4C2*7C4 - There are 8 men and 7 women. In how many ways a group of 5 people can be made such that at least 3 men are there in the group?
A) 1545
B) 1626
C) 1722
D) 1768
E) 1844C) 1722
Explanation:
Case 1: 3 men and 2 women
8C3*7C2 = 1176
Case 2: 4 men and 1 women
8C4*7C1 = 490
Case 3: all 5 men
8C5 = 56
Add all the cases. - There are 6 men and 7 women. In how many ways a committee of 4 members can be made such that a particular woman is always included.
A) 180
B) 120
C) 240
D) 220
E) 260D) 220
Explanation:
There are total 13 people, a particular woman is to be included, so now 12 people are left to chosen from and 3 members to be chosen. So ways are 12C3. - There are 5 men and 3 women. In how many ways a committee of 3 members can be made such that 2 particular men are always to be excluded.
A) 50
B) 20
C) 24
D) 48
E) None of theseB) 20
Explanation:
Total 8 people, 2 men are to excluded, so 6 men left to be chosen from and 3 members to be chosen. So ways are 6C3.
AffairsCloud Recommends Oliveboard Mock Test
AffairsCloud Ebook - Support Us to Grow
Govt Jobs by Category
Bank Jobs Notification