Aptitude Questions: Mensuration Set 9

Hello Aspirants. Welcome to Online Quantitative Aptitude section in AffairsCloud.com. Here we are creating question sample from Mensuration that are important for all the competitive exams. We have included some questions that are repeatedly asked in exams !!

1. A rectangular box has dimensions 1.6 m × 1 m × 0.6 m. How many cubical boxes each of side 20 cm can be fit inside the rectangular box?
   A) 220
   B) 205
   C) 120
   D) 165
   E) 124
   

   Answer & Explanation

   C) 120
   Explanation:
   20 cm = 0.2 m
   So number of boxes that can fit = 1.6 × 1 × 0.6/0.2 × 0.2 × 0.2
   
   
   
2. What is the volume of a cylinder whose curved surface area is 704 cm² and height is 14 cm?
   A) 2878 cm³
   B) 2914 cm³
   C) 2396 cm³
   D) 2816 cm³
   E) 2916 cm³
   

   Answer & Explanation

   D) 2816 cm³
   Explanation:
   2ᴨrh = 704, h = 14
   Solve both, so r = 8
   Volume = ᴨr²h
   
   
3. If the volume of wire remains the same but its radius decreases to 1/3rd of previous, then the new length of the wire will be how many times of the previous length?
   A) 3 times
   B) 4 times
   C) 6 times
   D) 10 times
   E) 9 times
   

   Answer & Explanation

   E) 9 times
   Explanation:
   Wire will be taken as cylinder.
   R = r/3
   ᴨr²h = ᴨR²H
   r²h = (r/3)²H
   so H = 9h
   
   
   
4. A cone with diameter of its base as 12 cm is formed by melting a spherical ball of diameter 6 cm. What is the height of the cone?
   A) 6 cm
   B) 3 cm
   C) 32 m
   D) 15 cm
   E) None of these
   

   Answer & Explanation

   B) 3 cm
   Explanation:
   Radius of cone = 12/2 = 6, radius of ball = 6/2 = 3
   Volumes will be equal, so
   (1/3)ᴨ r²h = (4/3)ᴨ R³
   6²h = 4* 3³
   So h = 3
   
   
5. The total cost of painting the walls of a room is Rs 475. Find the cost of painting the walls of another room whose length, breadth and height each are double than the dimensions of the previous room.
   A) Rs 1780
   B) Rs 1900
   C) Rs 1846
   D) Rs 1960
   E) Rs 1600
   

   Answer & Explanation

   B) Rs 1900
   Explanation:
   Area of first room = 2(l+b)*h
   After all dimensions doubled, new area = 2(2l+2b)*2h = 4[2(l+b)*h ] = 4 times previous area, so cost of painting = 4*475
   
   
   
6. A circular wire of diameter 84 cm is bent into a rectangle with sides ratio 6 : 5. What are the respective sides of the rectangle?
   A) 60 cm, 72 cm
   B) 78 cm, 65 cm
   C) 72 cm, 60 cm
   D) 90 cm, 75 cm
   E) None of these
   

   Answer & Explanation

   C) 72 cm, 60 cm
   Explanation:
   Length of wire = 2ᴨr = 2(22/7)*42 = 264 cm
   Perimeter of rectangle = 2(6x+5x) = 264
   Solve, x = 12
   So dimensions – 12*6, 12*5
   
   
   
7. The ratio of the outer and the inner perimeters of a circular path is 9 : 8. The path is 3 metres wide. What is the diameter of the outer circle?
   A) 20 m
   B) 27 m
   C) 35 m
   D) 39 m
   E) 24 m
   

   Answer & Explanation

   B) 27 m cm³
   Explanation:
   2ᴨr/2ᴨR = 9/8
   So r/R = 9/8, so r = (9/8)R
   r-R = 3, so (9/8)R – R = 3
   R = 24, so r = (9/8)*24 = 27
   
   
   
8. Four circular cardboard pieces, each of diameter 28 cm are placed in such a way that each piece touches two other pieces. Find the area of the space enclosed by the four pieces.
   A) 195 cm²
   B) 134 cm²
   C) 168 cm²
   D) 162 cm²
   E) None of these
   

   Answer & Explanation

   C) 168 cm²
   Explanation: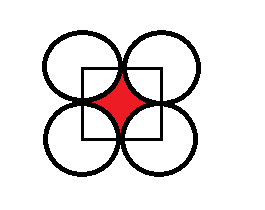
   Required area = area of square shown in figure – 4*areas of 1/4th parts of each circle, so
   Required area = 28*28 – 4*(1/4)*(22/7)*14*14
   
   
9. A solid sphere of radius 20 cm is melted to form 12 spherical balls. Find the radius of each of the ball.
   A) 12 cm
   B) 8 cm
   C) 20 cm
   D) 10 cm
   E) 15 cm
   

   Answer & Explanation

   D) 10 cm
   Explanation:
   Volume of each of the 8 ball = [(4/3)*(22/7)*20³]/8
   So (4/3)*(22/7)*r³ = [(4/3)*(22/7)*20³]/8
   Solve, r = 10
   
   
10. The perimeter of a rectangular plot is 210 m. Find the cost of gardening 2 m broad boundary around rectangular plot whose perimeter The cost of gardening is Rs 14 per m².
    A) Rs 6450
    B) Rs 6400
    C) Rs 6480
    D) Rs 6104
    E) Rs 6880
    

    Answer & Explanation

    D) Rs 6104
    Explanation:
    Given 2(l+b) = 210
    2 m broad boundary means increase in l and b by 4 m
    So area of the boundary will be [(l+4)(b+4) – lb] = 4(l+b) + 16 = 2*[2(l+b)] + 16 = 2*210 + 16 = 436 m²
    So cost of gardening = 436*14